元分析效益量提取-从娃娃抓起
引
新科学知识的增长固然很重要，对过往知识的总结也必不可少——元分析在社会科学里正在扮演越来越重要的角色。从医学、心理学再到经济管理、社会科学大类。这项方法真的算火出圈了。
元分析一开始就是个"苦力活"，文献筛选与效应量提取，似乎已经成为无数做元分析或系统性综述同学的噩梦1。而元分析半数以上的工作量就体现在这里。
本文将试图用最简单的语言，为第一次做元分析的选手提供效应量提取的思路2。力图让刚刚入门的同学，看到巨长的预注册文档与Code Sheet不再懵逼。
那么效应量(Effect Size)是啥？
效应量就是衡量总体中两个变量之间关系强度的值，或者是对该数量的基于样本的估计。它可以指从数据样本中计算出的统计值、假设总体的参数值，或用于操作统计或参数如何导致效应大小值的方程。
人话版本: 效应量就是衡量效果如何的指标，并且这个指标不受样本容量影响。举个栗子，不同地区的高考卷肯定难度不一样，两个不同地区的同学，同样考了500分，怎么比较哪个考的更好呢？我们就需要一个统一的指标来衡量他，这个指标就是"效应量"。通过一些转换，我们把全国所有省份的分数换到了一个统一的、可比的指标上。
效应量有三家
其实效应量大家已经见过以前学过的相关系数r，就是一种效应量，他不受到样本量的影响。两个r之间可以进行比较。
效应量也是所有元分析的基本指标和结果。元分析中常用的效应大小可分为三类：
-
基于r的效应量代表X和Y之间的相关性；
-
基于d的效应量代表X类别中Y的标准化平均差异；
-
基于odd的效应量，代表X类别中Y结果的比率或相对频率。
d-Based 效应量历史悠久，其实就是比较类别间的差异：比如为了对比午时茶和板蓝根哪个对感冒好用3，我们就可以算一个实验的效应量，比一比哪个更好。这里指的就是 午时茶和板蓝根 这个类别X，对 感冒康复 这个Y的效果。
r-Based 效应量很知名，但是近年才多起来。第一篇元分析的文章，就是用的r-Based效应量。作者卡尔·皮尔逊（Karl Pearson），也就是发明r相关系数的人。然而，相对较少的现代元分析分析采用基于r的效应量。其中一个重要原因是，在医学和心理学的实验传统中，相关系数往往是传递研究结果的不恰当指标（d-Based 效应量更适合）。r效应量适用于 连续变量X 与连续变量Y的情况。
相关系数是公共管理、公共政策和社会科学研究人员的常用工具。因此，这些领域的元分析应该采用基于r的效应大小。
odd-Based 效应量是当Y和X都使用二元指标进行测量时使用的效应量。这种情况在医学研究中很常见，研究人员通常对通过服用新药或安慰剂的治疗组和对照组之间的二分法结果（例如，心脏病发作）的频率感兴趣。
对于研究制定者，选择效应量应该具有良好的统计特性并应具有实质性的可解释性。
怎么算效应量？
r-Based 效应量
当文章没有直接报告r的情况下，使用以下对策：
如果文章使用t检验（如OLS回归）：
$$ r=\sqrt{\left[t^{2} /\left(t^{2}+d f\right)\right]} $$
其中 df= n - k - 1 （k是回归中变量的数量）
t检验一般报告在回归表里，如果没有报告t的话，也可以通过回归系数和标准误来算：
$$ \begin{aligned} t &=b_{j} / s_{b j} \ r &=\sqrt{\left[t^{2} /\left(t^{2}+d f\right)\right]} \end{aligned} $$
其中b就是回归系数beta，s就是Standard Error.
例子（beta / se）：
这一列系数的底下就是SE。
如果文章用Logit （或者其他使用ML估计的模型）:
这类回归表里会报告Wald检验或者Z检验，如这样：
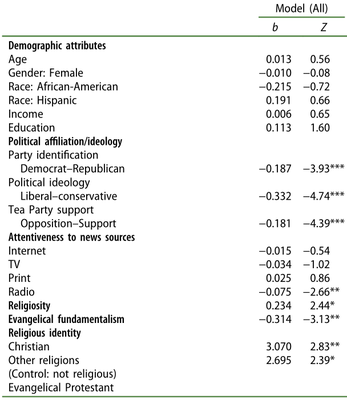
咱们要的，就是这个Z或者Wald：
$$ r=\sqrt{\left[Z^{2} / n\right]} \quad r=\sqrt{\left[X_{1}^{2} / n\right]} $$
注意：拿到t，除了需要N以外，还需要计算df，才能转换成r。但是拿到Z或者Wald只需要N就行了。
如果文章只给了*或者p来代表显著性呢？
把*代表的显著性程度记录下来，将t设置为符号阈值和给定自由度下的t值。例如，如果一项原始研究报告b=1.50**，其中n=54，k=3，且**p<0.05，则t=2.009；也就是说，p | t(50)>2.009=0.05。使用这些t值计算的偏相关系数代表下限, 实际的偏相关系数会更大，但如果没有额外的信息，我们无法判断其大小。
如果文章只说了不显著呢？
建议把效应量设置为0，因为无视这些研究会导致总体的高估（毕竟人家都说了不显著了）。
r-Based 效应量的方差
知道了r以后，r的变动也是很关键的。使用提取出的r与N就可以算出来：
$$ V[r]=\left(1-r^{2}\right)^{2} /(n-1) $$
d-Based 效应量
d-Based效应量一般都是做实验的，一个控制组一个实验组这样的研究。有以下几种情况
如果报告了实验组和控制组的均值和标准差
拿着实验组、控制组均值，带上标准差，直接算就行：
$$ d=\left(Y_{1}-Y_{2}\right)/S_{\text{Pooled}} $$
$$ S_{\text {Pooled }}=\sqrt{\left[\left(\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}\right) /\left(n_{1}+n_{2}-2\right)\right]} $$
（不过做元分析，只需要提取出来就好，计算肯定是后面统一算的）
如果报告了两个均值之差的显著性
把对于的t，Z，F检验拿出来就行。对于DID的情况，如果t没有直接报告，可以用之前的b/se的方法算。
$$ d=t \sqrt{\left[\left(n_{1}+n_{2}\right) / n_{1} n_{2}\right]} $$
$$ d=Z \sqrt{\left[\left(n_{1}+n_{2}\right) / n_{1} n_{2}\right]} $$
$$ d=\sqrt{\left[F\left(n_{1}+n_{2}\right) / n_{1} n_{2}\right]} $$
这一类其实涵盖了很多模型(回归、ANOVA等等都用上述的检验)
如果报告了p，而没有报告t的情况
对于双尾t检验，拿到p就可以了（注意如果只用了*，就取显著性的阈值）：
$$ d=+/-t^{-1}(p / 2) \sqrt{\left[\left(n_{1}+n_{2}\right) / n_{1} n_{2}\right]} $$
d-Based效应量的方差
拿到d和N以后，真的一切都好说了
$$ V[d]=\left(\left(n_{1}+n_{2}\right) / n_{1} n_{2}\right)+\left(d^{2} / 2\left(n_{1}+n_{2}\right)\right) $$
这三家其实还有很多亲戚
比如Hedge’s g是d效应量的修正，Fishers’z 是r的进化版…这些关系都可以被轻易的转化。
查看这个效应量转化Cheatsheet获得更多的信息。
一些计算资源
除了R以外，还有很多很好的在线计算网站：
https://www.campbellcollaboration.org/escalc/html/EffectSizeCalculator-SMD21.php
https://www.psychometrica.de/effect_size.html#transform
The End
祝大家元分析顺利！
Ziqian Xia (夏子谦)
Graduate Student
My research interests include Environmental Behaviour、Environmental Economics and Meta Science.